Data Structure and Algorithm (DSA) has always been a buzzword in the industry. With all the hype being created around it some people are terrified to even go near it. (I used to be "some people").

I am a self-taught programmer and I'm taking you along my journey of mastering the Data Structure and Algorithm. This article serves as an entry point for someone very new to the subject and also provides a wide picture of what else to expect in the future.
Before anything let's start with the question.

What is Data?

Data refers to raw, unprocessed facts, figures, symbols, or information on which operations are performed by a computer, which can be stored, transmitted, or processed.
Well, that was vague but bear with me!
So, data can be anything for example numbers, text, images, audio, video.

When does the data become information?

When data is arranged systematically then it gets a structure and becomes meaningful. This meaningful or processed data is called information.

Let's understand this with the help of the example below:

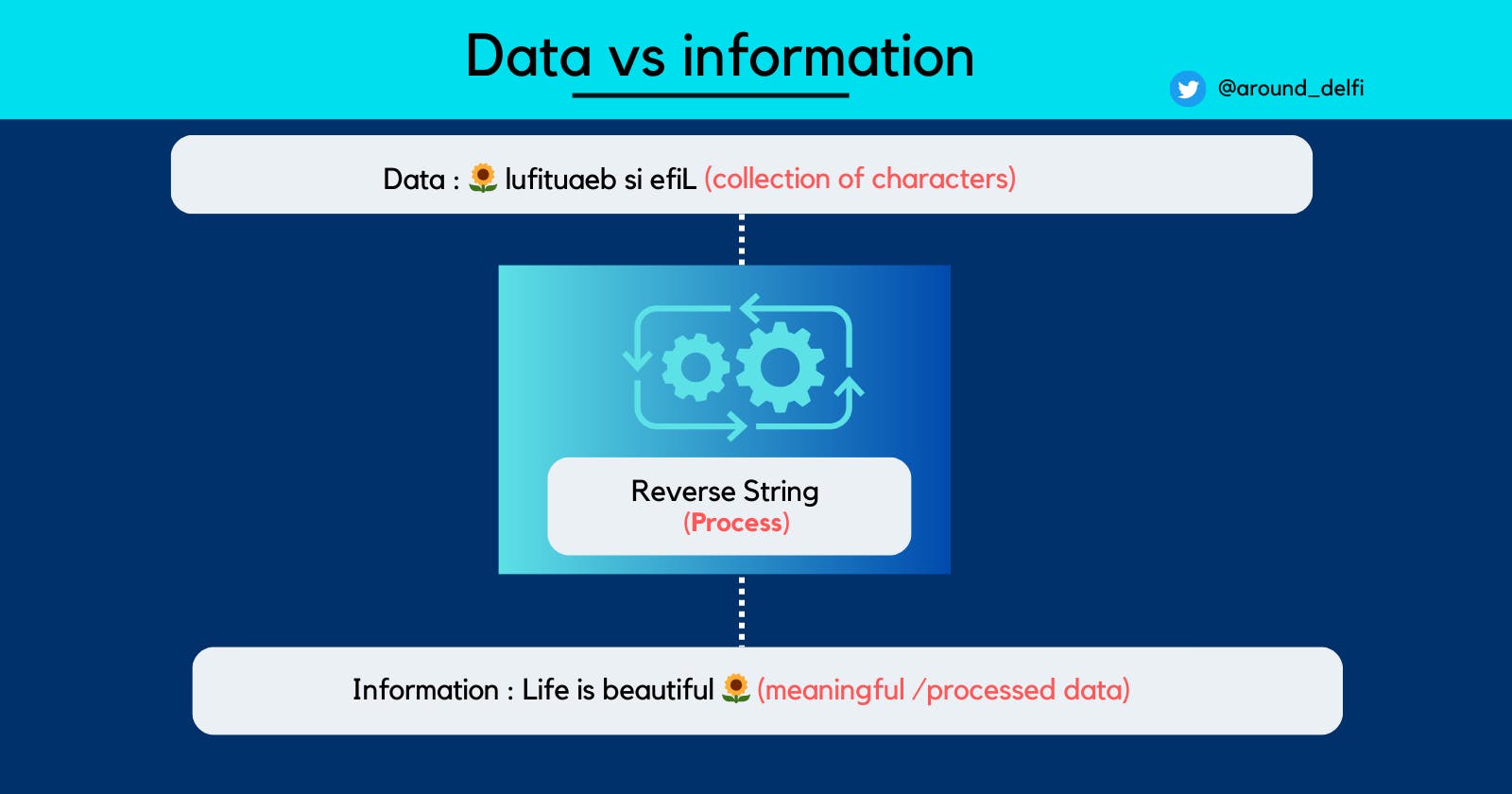
Here, we understand that data needs to be arranged, managed, or structured in a certain way for it to produce meaningful information.
Hence, to provide an appropriate way to structure data we need Data structures.

Data Structures

The data structure is a systematic way of organizing and storing different types of data in the main memory so that it can be accessed and manipulated efficiently. Efficiency here is measured in terms of Time and Space which we will cover later.
It provides a means to manage and structure data to perform operations like insertion, deletion, searching, and sorting effectively. Data structures act as the building blocks for algorithms. It defines the layout of data elements and the operations that can be performed on those elements.

Common examples of data structures include arrays, linked lists, stacks, queues, trees, graphs, and hash tables.
(If you are unfamiliar with these data structures, don't worry I'll be covering each one of them in separate articles in detail.)

Each data structure has its own strengths and weaknesses, making them suitable for specific types of tasks. The choice entirely depends upon user requirements.

Here are some of the critical things specified by a data structure:

Data Organization: Data structures specify how data elements are organized and stored. This includes how individual elements are grouped together and the relationships between them.
Access Methods: Data structures specify how data can be accessed. This includes defining methods for inserting, retrieving, updating, and deleting data elements. Access methods may vary depending on the specific data structure.
Memory Allocation: Data structures dictate how memory is allocated and managed to store the data elements. They specify how memory is reserved for data storage and how it is released when no longer needed.
Efficiency: Data structures aim to provide efficient ways of performing common operations. They specify the time and space complexity of operations like insertion, deletion, searching, and sorting, helping developers choose the right data structure for their needs.
Relationships: Data structures define the relationships between data elements, such as parent-child relationships in trees or adjacency relationships in graphs. These relationships are crucial for various algorithms and operations.

Classification of Data Structure

Broadly, Data structures can be classified into the following two categories:

1. Primitive Data Structure

Primitive data structures are the basic types of data that computers understand without needing extra instructions. They are the building blocks for more complex data structures used in programming.
They include:

Integers: For whole numbers like 1, -5, and 100.
Floating-Point: For numbers with decimals, like 3.14 or -0.001.
Characters: For single letters, digits, or symbols, like 'A', '7', or '$'.
Boolean: For true or false values, used in logic.

2. Non-Primitive Data Structure

They are complex Data structures responsible for organizing groups of homogenous and heterogenous data elements. These are developed from primitive data Structures.
Example: Arrays, Lists, Tree

It can further be classified into the following two types:

2.1. Linear Data Structures

A data structure is called linear if its elements are arranged in a linear or sequential order. In a non-hierarchical way, each element has a successor and predecessor except the first and last element. It's important to note that this linear arrangement doesn't necessarily correspond to sequential memory allocation.
example: array, stack, queue, and linked list.

Linear Data Structures can be classified into two categories based on memory allocation:

Static Data Structures: These data structures have a fixed size predetermined at compile time. Users cannot change the size after compilation, but they can modify the data stored within them. A prime example is an Array, which has a fixed size that can't be altered once defined, but the data it holds can be updated.
Dynamic Data Structures: Dynamic Data Structures, on the other hand, have a size that can change during runtime. Memory for these structures is allocated as the program runs, and users have the flexibility to adjust both the size and the data elements within them while the code is executing. Common examples include Linked Lists, Stacks, and Queues.

2.2. Non-linear data structures

A data structure is called non-linear if its elements are not arranged in a linear or sequential order.
(Makes sense right? but what does this mean?)
This data structure does not form a sequence in which each item or element is connected with two or more other items in a non-linear arrangement. the data elements are not arranged in a sequential structure.

When data elements are organized in some arbitrary function without any sequence such data structures are called non-linear data structures.
Examples: trees, graphs.

Operations of Data Structure

Data structures support various operations that allow you to manipulate the data they contain efficiently. The specific operations depend on the type of data structure you're working with. Here are some common operations associated with data structures:

Search: Finding a particular data element within the structure. This operation is commonly used to look for a specific value, key, or node.
Traversal: Visiting all data elements in the structure in a specific order. Common traversal methods include in-order, pre-order, and post-order traversals in binary trees or iterating through all elements in an array.
Insertion: Adding new data elements to the structure. For example, adding an item to an array, appending a node to a linked list, or inserting a key-value pair into a hash table.
Update: Changing the value of a data element or updating its attributes. For example, updating an element in an array or changing the value associated with a key in a dictionary.
Deletion: Removing data elements from the structure. This might involve removing an item from an array, deleting a node from a linked list, or removing a key-value pair from a hash table.
Merging: Combining two or more data structures into one. This operation is common in merge sort or when merging two sorted lists.
Sorting: Arranging the elements within the data structure in a specific order, such as ascending or descending. Sorting is often needed for efficient searching and retrieval.

Advantages of Data Structures:

Efficiency: Data structures help your programs run faster and use memory wisely. They make common tasks like finding data or adding new information quicker and easier.
Reusability: Once you create a data structure, you can use it again and again in different parts of your code or even in other projects. It saves you time and effort.
Abstraction: Data structures hide complicated details, making your code easier to read and understand. You can focus on solving problems without getting bogged down by low-level stuff.

Algorithm

An algorithm is a step-by-step set of instructions or a sequence of well-defined actions that are executed to solve a specific problem or perform a particular task. Algorithms are crucial for achieving desired outcomes and are independent of the programming language used to implement them.

Algorithms can perform various tasks, such as searching for an item in a list, sorting a list of elements, finding the shortest path in a graph, and much more. The efficiency and correctness of an algorithm are critical, as they determine how quickly and accurately a task can be completed.

Data structures and algorithms are closely related - you choose an algorithm to complete a specific task, and then implement that algorithm using some data structure. Well-chosen data structures allow for efficient algorithms, which help you solve computational problems.

How to define an Algorithm?

1. Clearly define the problem statement, input, and output
2. The steps in the algorithm need to be in specific order.
3. The steps also need to be distinct. (You shouldn't be able to break it down into further subtasks).
4. The algorithm should produce a result.
5. The algorithm should be completed in a finite amount of time.
6. It should produce consistent results for the same set of values.

Example: Write an algorithm for the sum of two numbers
Step 1: Start

Step 2: Input the first number (num1)

Step 3: Input the second number (num2)

Step 4: Calculate the sum = num1 + num2

Step 5: Output the sum

Step 6: End

First, we break down the problem into any possible number of smaller problems where each of them can be clearly defined in terms of input and output. It is a very important concept of algorithmic thinking.

So, An algorithm possesses the following properties:

Finiteness: An algorithm must terminate after a finite number of steps. It cannot run indefinitely. This property ensures that the algorithm eventually produces a result.
Definiteness: Each step of an algorithm must be precisely defined and unambiguous. There should be no ambiguity or confusion in how to perform each step.
Input: An algorithm takes zero or more inputs as parameters. These inputs provide the initial data on which the algorithm operates. Input values can vary, and the algorithm should handle different inputs correctly.
Output: An algorithm produces at least one output as a result. The output could be a solution to a problem, a value, a decision, or some other form of data. The output should be well-defined and related to the inputs.
Effectiveness: An algorithm should be effective, meaning it can be implemented and executed in practice using a finite amount of resources (time and memory). It should not be purely theoretical but should be applicable in real-world scenarios.
Determinism: Given the same input, an algorithm should always produce the same output. The outcome of an algorithm should be predictable and consistent.

What makes a good algorithm?

There is no universal truth to measure if it is the best solution because it all depends on the context. A good algorithm exhibits key characteristics that make it effective and efficient for solving specific problems. Here are the qualities that contribute to a good algorithm:

Correctness: An algorithm is deemed correct if on every run of the algorithm against all possible values of the input data we always get the expected output.
A good algorithm must produce correct results for all valid inputs. It should accurately solve the problem it was designed for without errors or unexpected behaviors.
Efficiency: An efficient algorithm accomplishes its task in a reasonable amount of time and uses a reasonable amount of resources, such as memory. This includes optimizing time complexity (fast execution) and space complexity (minimal memory usage).
Clarity and Simplicity: A good algorithm is easy to understand, both in terms of its logic and its implementation. Simple algorithms are less error-prone and more maintainable. They should have clear and concise descriptions.
Scalability: It should work efficiently even as the size of the input data or problem complexity increases. Scalable algorithms can handle both small and large datasets.
Maintainability: Algorithms should be designed and implemented in a way that makes them easy to modify and maintain as requirements change or as improvements become necessary.

Efficiency of an Algorithm

Remember that this efficiency ultimately matters because it helps us solve a problem faster and deliver a better end-user experience in a variety of fields.

There are two major measures of efficiency when it comes to an algorithm: Time and Space. Efficiency is measured by time, something you will hear Time complexity is a measure of how long it takes an Algorithm to run. It translates to the less time you take the more efficient you are.
Another measure of efficiency is Space complexity. It deals with the amount of memory taken up on a computer.
A good algorithm needs to balance between these two measures to be useful. For example, you have a lightning-fast algorithm but it's useless if it requires more memory than you have available.
Both of these Space-Time complexity is measured using various metrics and notations such as Big O Notation (Worst Case), Theta Notation (Average Case), and Omega Notation (Best Case) all of which fall under Algorithm Analysis.

Algorithm analysis

The process of determining the amount of resources required, such as time and space by correct algorithm is called algorithm analysis. The amount of time that any algorithm takes to run almost always depends on the amount of input that it must process.
For example, sorting 10 elements is expected to take less time than sorting 10,000 elements. The running time of an algorithm is thus a function of the input size. The exact value of a function depends on many factors such as the speed of the host machine, the quality of the compiler, and in some cases the quality of the program.
The primary goals of algorithm analysis are to:

Measure Complexity: Determine how an algorithm's performance scales with respect to the size of the input data. This includes understanding the worst-case, average-case, and best-case scenarios.
Compare Algorithms: Compare different algorithms to identify the most suitable one for a particular problem based on its efficiency and resource usage.
Optimize Algorithms: Identify opportunities for optimizing existing algorithms by reducing time and space complexity or making other improvements.

Key aspects of algorithm analysis include:

Time Complexity Analysis: This involves analyzing how the running time of an algorithm increases as the size of the input data grows. The result is typically expressed using Big O notation, which describes an upper bound on the algorithm's time complexity. Common complexities include O(1) for constant time, O(log n) for logarithmic time, O(n) for linear time, O(n log n) for linearithmic time, and O(n^2) for quadratic time, among others.
Space Complexity Analysis: Space complexity measures how much additional memory an algorithm needs relative to the input size. It is also expressed using Big O notation, with common complexities such as O(1) for constant space and O(n) for linear space.
Worst-Case, Average-Case, and Best-Case Scenarios: Algorithms can have different performance characteristics depending on the input data. Analyzing these scenarios helps understand how an algorithm behaves under various conditions.

Did you catch that?
In our article, we've been talking a lot about the efficiency of algorithms, and it's a crucial topic that we'll explore further in upcoming articles. This will include a deep dive into Algorithm Analysis, so if it all feels a bit overwhelming right now, don't fret.

I hope you found the article useful, and there's more exciting stuff coming your way! Keep an eye out for our future articles where we'll delve even deeper into data structure and algorithm concepts. Happy learning! 😊

delfina's blog